Generative Adversarial Nets

Generative Adversarial Nets

• Link : https://arxiv.org/abs/1406.2661

Abstract

이 논문에서는 경쟁을 통해 Generative model을 훈련시키는 새로운 프레임워크를 제시한다. 경쟁은 Generative model G와 Discriminative model D 사이에서 이뤄지는데, G는 실제 데이터의 분포를 모사하는 모델이고, D는 데이터 $x$가 주워졌을 때, $x$가 G가 생성한 데이터 분포에서 sampling된건지, 실제 데이터인지 구별하는 모델이다.

모델 G의 학습 목적은 D가 잘못 판단할 확률을 최대화시키는 것으로, 이러한 프레임워크는 minimax two-player game과 같다.

임의의 함수 G와 D에 대해, unique한 solution이 존재하며 그 solution은 G가 training data를 완벽히 모사하여, D가 데이터를 구분해낼 확률이 1/2일 때이다.(찍는 것과 같다)

G와 D가 multilayer perceptrons일 경우, 전체 시스템은 Markov chains나 unrolled approximate inference networks없이 backpropagation으로 학습이 가능하다.

1 Introduction

Backpropagation과 dropout과 같은 주요 알고리즘 덕에 Deep Learing에서도 특히 Discriminative model이 큰 성공을 이뤘다.

• Discriminative model은 고차원의 많은 정보가 담긴 데이터에 class label을 mapping하는 모델을 말한다.

하지만 Deep generative model에서는 처리하기 어려운 probablistic computation으로 인해 그 영향이 적었는데, 이 논문에서는 이러한 어려움들을 피하는 새로운 generative model 추정 과정을 제안한다.

Adversarial nets framework에서 generative model은 discriminative model을 적으로 상대하는데, discriminative model은 sample이 model distribution에서 나온건지, data distribution에서 나온건지 구별하도록 학습한다.

Generative model을 진짜인지 가짜인지 식별되지 않는 가짜 통화를 ‘제조’하려고 하는 사기꾼이라 한다면, discriminative model은 사기꾼이 만든 가짜 통화를 ‘식별’하려고 하는 경찰이라 비유할 수 있다.

둘의 경쟁은 진짜 통화와 가짜 통화가 더 이상 구별이 되지 않을 때까지 이뤄지며, 그동안 사기꾼의 가짜 통화 ‘제조’방법과 경찰의 가짜 통화 ‘식별’방법은 개선되게 된다.

이런 (경쟁)프레임워크는 많은 모델의 구체적인 학습 알고리즘과 최적화 알고리즘을 만들어낼 수 있다.

이 논문에서는 multilayer perceptron인 generative model의 input으로 random noise를 넣어 sample을 만들고, discriminative model 또한 multilayer perceptron인 특별한 케이스를 탐색해보고자 한다.

우리는 이런 특별한 케이스를 Adversarial Nets라 한다.

이 경우에, 두 모델 모두 오직 backpropagtion과 dropout 알고리즘만을 이용해서 훈련시키고, froward propagtion만으로 generative model으로 sample을 만들 수 있다.

Adversarial nets

Adversarial modeling framework는 모델들이 모두 multilayer perceptrons(deep learning models)일 때 효과적이다.

• 데이터 $x$에 대한 generator의 distribution을 $p_g$
• input noise 변수를 $p_z(z)$
• $p_z(z)$를 data space에 mapping 하는 모델 $G(z:\theta_g)$

G는 $\theta_g$로 이루어진 multilayer perceptron 모델이며, $D(x;\theta_d)$ 또한 multilayer perceptron으로 x가 $p_g$가 아닌 real data의 데이터일 확률을 single scalar로 출력한다.

Training example G가 만든 samples에 대해 D가 label을 정확하게 부여할 확률을 최대화하도록 D를 훈련시키는 동시에, G는 $log(1-D(G(z)))$를 최소화하도록 훈련시킨다.

G가 $log(1-D(G(z)))$를 최소화시키도록 훈련시킨다는 것은 D가 $G(z)$를 1에 가깝도록 훈련시킨다는 것이고, 이는 G가 $z$가 real data로 분류될 확률을 최대화하도록 훈련시킨다는 것이다.

$\underset{G}{min}\ \underset{D}{max}V(D,G) = E_{x\sim p_{data(x)}}[logD(x)]+E_{z\sim p_{z(z)}}[log(1-D(G(z)))]$

Adversarial nets의 이론적인 분석을 살펴보자. 여기서는 D와 G의 학습 과정을 보여준다.

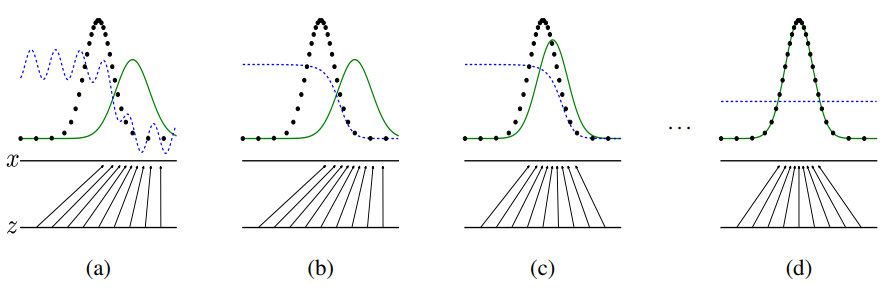
(a) 학습이 되지 않은 초기 상태이다. $p_g$와 $p_{data}$의 형태가 비슷한 정도이며, discriminative function이 데이터를 부분적으로 정확하게 분류함을 알 수 있다.

(b) D의 알고리즘 내부에서 D가 데이터의 sample을 식별하도록 학습될 수 있게, D가 $D^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$(=data x가 G가 만든 데이터일지, 실제 데이터일지에 대한 확률)로 수렴하도록 학습된다.

(c) G를 학습시킨다. 이때, D의 gradient가 G(z)가 실제 데이터로 분류되게끔 학습되도록 학습시킨다.

(d) 이렇게 학습의 과정을 거치다 보면, 즉 G와 D가 충분한 능력이 되면 둘의 성능이 더 이상 향상되지 못하는 포인트에 다다른다. 그 이유는 $p_g=p_{data}$가 되어, discriminator가 더 이상 두 개의 분포를 구분하지 못하는 $D(x)=\frac{1}{2}$가 되기 때문이다.

• $D(x)=\frac{1}{2}$라는 것은, D가 데이터가 진짜인지 가짜인지 구분하는게 찍는거나 다름없다는 뜻이다. 즉, 진짜일 확률과 가짜일 확률이 50%대 50%라는 것

학습 과정의 inner loop에서 D가 최적화되도록 계속 학습시키는 건, 계산적으로 불가능하고 overfitting이 될 수 있다. 대신에 D를 k번 학습하고, G를 1번 학습하는 방식을 사용하면, D가 optimal한 solution에 가깝도록 유지할 수 있고, 이를 통해 G가 충분히 천천히 향상되도록 학습시킬 수 있다.

학습 초반에는 G의 성능이 형편 없는데, 이때는 D가 data를 너무 잘 구별해버려서 $log(1-D(G(z)))$가 saturate(포화)되어 gradient값이 너무 작아, 학습이 잘 되지 않는다. 따라서, G가 $log(1-D(G(z)))$를 최소화시키도록 하는 것보다, G가 $D(G(z))$를 최대화하도록 훈련시키면, 학습 초반에 더 높은 gradient를 바탕으로 학습의 효율을 높일 수 있다.

4 Theoretical Results

4.1 Global Optimality of $p_g=p_{data}$

minmax game이 $p_g=p_{data}$의 global optimum을 가지고 있음을 증명한다. 즉, $\underset{G}{min}\ \underset{D}{max}V(D,G)$식이 $p_g=p_{data}$가 되도록 학습될 수 있음을 보인다.

Proposition 1.

고정된 G가 있을 때, 최적의 discriminator D는 $D^*G(x)=\frac{p{data}(x)}{p_{data}(x)+p_g(x)}$가 된다.

Proof. 어떤 고정된 G가 있을 때, discriminator D의 training criterion은 $V(G,D)$를 최댓값으로 만드는 것이다. $V(G,D)= \int_{x}^{}p_{data}(x)log(D(x))dx\ + \ \int_{z}^{}p_{z}(z)log(1-D(g(z)))dz\ = \ \int_{x}^{}p_{data}(x)log(D(x))\ +\ p_{x}(x)log(1-D((x)))dx$

이 식이 최댓값을 가질 때의 $D(x)$값을 찾기 위해 미분한다. $V(G,D)$는 $y\rightarrow a\ log(y)+b\ log(1-y)$의 형태로, 미분하면 $a/y - b/(1-y)$가 나오고, 이 식을 $y$에 대해 정리하면, $y=a/(a+b)$가 나온다. $a=p_{data}(x), \ b=p_g(x)$이므로, $D(x)=p_{data}(x)/(p_{data}(x)+p_g(x))$일때 최댓값을 가진다.

D를 학습시키는 목적은 조건부확률 $P(Y=y

x)$의 log-likelihood를 최대화하는 것이라 해석할 수 있는데, 이때 $Y$는 $x$가 $p_{data}(y=1)$에서 온건지, $p_g(y=0)$에서 온건지를 나타낸다.

따라서, $\underset{G}{min}\ \underset{D}{max}V(D,G)$ 식은 다음과 같이 다시 쓸 수 있다.

$C(G) = \underset{D}{max}V(G,D) = E_{x \sim p_{data}}[log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}] + E_{x \sim p_g}[log\frac{p_g(x)}{p_{data}(x)+p_g(x)}]$

Theorem 1.

$C(G)$의 학습 기준(training criterion)의 global minimu값은 $p_g=p_{data}$일때만 얻어진다. 이때, $C(G)=-log4$이다.

Proof.

$p_g=p_{data}$일 때, $D^_G(x)=\frac{1}{2}$ 값을 가진다. ($D^G(x)=p{data}(x)/(p_{data}(x)+p_g(x))$)

따라서, $C(G)=log\frac{1}{2}+log\frac{1}{2}=-log4$가 된다.

즉, $C(G)$의 global minimum값이 $-log4$가 되고, G가 실제 data의 distribution을 완벽하게 모사할 때 ($p_g=p_{data}$) 얻어질 수 있다.

6 Advantages and disadvantages

Disadvantages

1) $p_g(x)$에 대한 명시적인 표현이 존재하지 않는다.

2) 훈련 중 D와 G가 서로 잘 동기화 되어야 한다. 즉, D가 학습되기 전에 G가 너무 빨리 많이 학습되어서는 안된다. D의 가중치가 업데이트 되기 전에 G의 가중치만 너무 많이 업데이트 되면, G가 $p_{data}$의 분포를 따라는데 충분한 다양성을 지니지 못하게 되어 ‘Helvetica scenario’에 빠지게 될 수도 있다.

Adavantages

1) backpropagation으로 gradient를 구할 수 있어 Markov chain이 필요하지 않다.

2) 학습 중 inference를 할 필요가 없다.

3) 다양한 함수와 Adversarian nets framework를 합칠 수 있다.

4) Generator network가 data sample을 바탕으로 직접 업데이트 되는게 아닌, discriminator를 통해 얻은 gradient로 업데이트를 진행하여 statistical advantage를 얻을 수 있다.

7 Conclusions and future work

• G, D에 c를 input으로 추가하면, Conditional Generative Model $p(x

  c)$을 얻을 수 있다.

• Auxiliary network가 $x$를 가지고 $z$를 예측하도록 훈련하여 Learned approximate inference를 수행할 수 있다.

• Parameters를 공유하는 conditional model을 학습하여, $x$의 모든 부분집합 $S$에 대해 조건부확률 $p(x_s

  x_{\not{s}})$를 얻을 수 있다.

• Semi-supervised learning : labeled 데이터가 적을 때 discriminator나 inference net에서 얻은 features로 classifier의 성능을 향상시킬 수 있다.
• Efficiency improvements : G와 D를 조정하는 더 좋은 방법을 고안하거나 훈련 시 $z$를 sample하는 더 좋은 방식을 정하여 학습 속도를 크게 가속화시킬 수 있다.

이 논문은 adversarial modeling framework의 실용 가능성을 증명하였고, 이 연구의 방향성이 유용함을 시사한다.